Balancing Continuity and Survival: Lessons for Overseas Manufacturers from Thailand’s 2001 Flood
【Updated : Disaster Link Library launched (website)】
【Project launched (website)】Disaster Risk Management in Aging Societies: Bridging Japanese Experience with Thai Policy Needs
【Disaster Research: Infograph】AI-Integrated Disaster Preparedness Platforms (Open Access Examples)
The infographic of the AI-Integrated Disaster Preparedness Platforms is shown as an infographic: AI-Integrated Disaster Preparedness Platforms
【Disaster Research: Infograph】Global Trends of Disasters
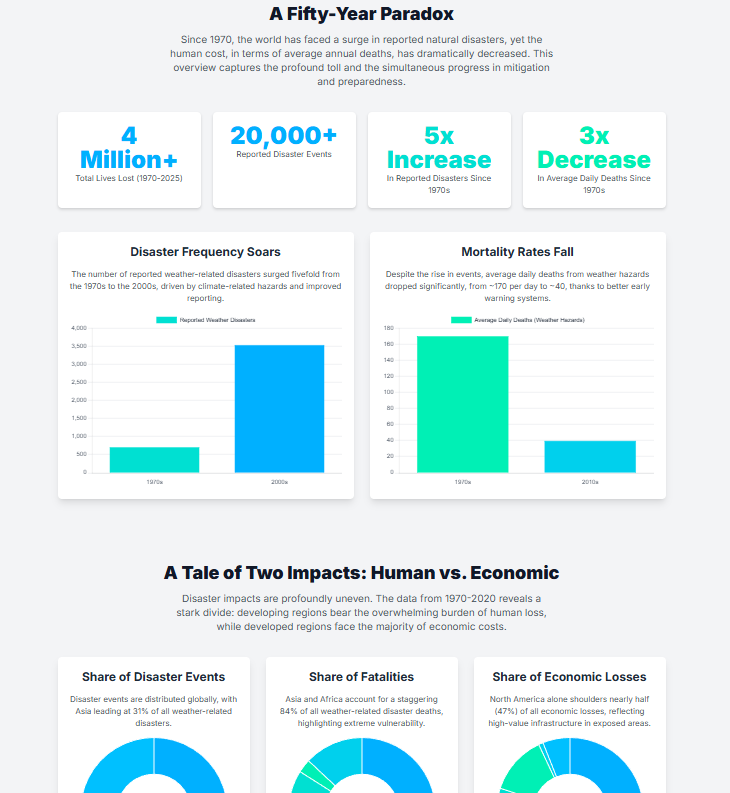
The infographic of the global trends of disasters (1970-2025) is shown as an infographic: https://disasters.weblike.jp/global%20trends.html
【Disaster Research: website】Logistic Regression Analysis (Simply explained)
The website of the logistic regression analysis in the demography and public policy seminar. Created one of the simplest and easiest-to-understand websites.
website:https://disasters.weblike.jp/logistic%20regression%20overview.html
【Disaster Research: Infograph】Demography and Public Policy Relationship
The infographic of the demography and public policy seminar, one example slide, is shown as an infographic: https://disasters.weblike.jp/IVDV_Relationship%20v1.html
【Disaster Research: Infograph】1985 mexico city earthquake
The infographic of the 1985 Mexico City Earthquake, mainly focusing on the social factors with earthquake characteristics, is shown as an infographic: http://disasters.weblike.jp/mexico%20infogr.html
The distance impact reminded me of the situation in Bangkok when an earthquake occurred in Myanmar in April 2025.
【Disaster Research: Infograph】The 2004 Tsunami in Thailand
This infographic was presented at RIHN in Japan as part of the Prof. Ito project, as part of the Feasibility Study. The infographic website is: https://disasters.weblike.jp/IOT%20v2.html
The presented numbers should be confirmed. Especially, the foreigner’s death toll and the Thai national death toll, with their proportion, are under reinvestigation.
【Disaster Research : Infograph】Thailand’s Demographic Transformation
An infographic, “Thailand’s Demographic Transformation,” was created.https://disasters.weblike.jp/Thai%20demographic%20change.html